 |
| De gulden snede wordt ook wel ‘gouden verdeling’ (sectio aurea), ''gulden regel'' (ratio aurea) of ‘goddelijke verhouding’ (proportio divina) genoemd. De gulden snede is om verschillende redenen interessant. Ten eerste is het een klassieke opvatting dat de Gulden Snede "mooie" verhoudingen geeft. Al in de oudheid baseerden de Grieken, al dan niet bewust, de ontwerpen van gebouwen op de Gulden Snede. Later kwam dit concept opnieuw in de mode in de Renaissance, en ook vandaag de dag zijn er kunstenaars en architecten die de Gulden Snede toepassen in hun werk om tot een mooie compositie te komen. |
  Voorbeelden uit de oudheid zijn: Voorbeelden uit de oudheid zijn:
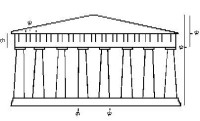
Het beroemde Parthenon (tempel va de Griekse god Athene) is gebouwd rond 440 voor Christus. Daarin kun je ook de Gulden Snede terug vinden. |
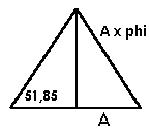
De oude Egyptenaren bouwden piramides die als begraafplaats gebruikt werden. Naast architectonisch onderzoek worden er ook wiskundige onderzoeken gedaan. Zo blijkt dat de Gulden Snede een grote rol speelt in de bouw van een piramide. We nemen nu de grote piramide in Gireh (gebouwd rond 2500 voor Christus) als voorbeeld. De hellingshoek van deze piramide is 51,85°. Wanneer we een dwarsdoorsnede van de piramide op de volgende manier maken dan krijgen we een driehoek. Als je nu de basis van de driehoek lengte A geeft, dan is de lengte van de schuine lijn: A * phi. Dus de Gulden Snede komt ook terug in de piramides.
|
| Ook in de klassieke schilderkunst wordt de gulden snede toegepast. Het wordt bijvoorbeeld gebruikt om de lengte-breedte verhouding van een schilderij te bepalen. Ook bij het definieren van de locatie van het aandachtspunt wordt de gulden snede gebruikt. |
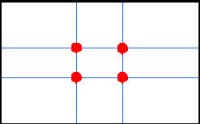  Vroeger had men nog nooit gehoord van de guldensnede maar toch tekenden ze hun schilderijen in hun onderbewustzijn wel op de gulden snede. Van nature zoekt het oog deze plek op. In een rechthoekig vlak kan dit punt op vier plaatsen gevonden worden (zie de rode punten rechts boven, links boven, links onder, rechts onder). Vroeger had men nog nooit gehoord van de guldensnede maar toch tekenden ze hun schilderijen in hun onderbewustzijn wel op de gulden snede. Van nature zoekt het oog deze plek op. In een rechthoekig vlak kan dit punt op vier plaatsen gevonden worden (zie de rode punten rechts boven, links boven, links onder, rechts onder).Rechthoeken met deze verhouding en de bijbehorende vierkanten komen veelvuldig voor in het schilderwerk van Piet Mondriaan. Overigens heeft Mondriaan, naar eigen zeggen, nooit gerekend aan zijn werken.
|
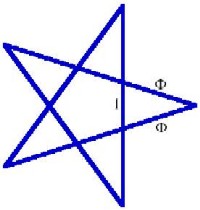 De Gulden Snede heeft een aantal interessante wiskundige eigenschappen: De Gulden Snede heeft een aantal interessante wiskundige eigenschappen:De Gulden Snede leidt tot een gelijkvormige vlakverdeling. De Gulden Snede blijkt voor te komen in figuren met vijfvoudige symmetrie. Teken maar eens een regelmatig pentagram. Elk van de vijf driehoeken is een gelijkbenige driehoek waarvan de zijden zich verhouden als 1 : φ (= φ : 1). |
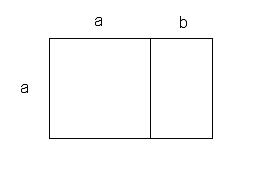
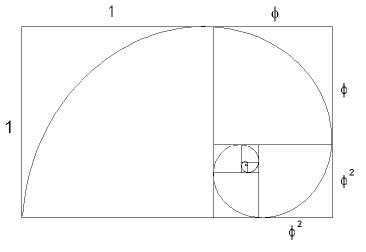 Een bijzonder rechthoek is de gulden rechthoek. De gulden snede maakt in deze rechthoek een bijzondere vlakverdeling mogelijk, namelijk een waarbij uitsluitend vierkanten van verschillende grootte worden gebruikt. Kijk eens naar het plaatje hiernaast. We beginnen met een rechthoek met lengte 1 + φ en breedte 1. We knippen aan de linkerkant een vierkant met zijde 1 weg, en houden rechts een rechthoek met lengte 1 en breedte φ over. Is nu φ gelijk aan de gulden snede (φ is ongeveer 1,61803... ), dan is de kleinere rechthoek gelijkvormig met zijn voorganger! Een rechthoek met deze lengte-breedteverhouding noemen we een gulden rechthoek. De kleinere gulden rechthoek kunnen we wéér verdelen in een vierkant en een nog kleinere gulden rechthoek. Een bijzonder rechthoek is de gulden rechthoek. De gulden snede maakt in deze rechthoek een bijzondere vlakverdeling mogelijk, namelijk een waarbij uitsluitend vierkanten van verschillende grootte worden gebruikt. Kijk eens naar het plaatje hiernaast. We beginnen met een rechthoek met lengte 1 + φ en breedte 1. We knippen aan de linkerkant een vierkant met zijde 1 weg, en houden rechts een rechthoek met lengte 1 en breedte φ over. Is nu φ gelijk aan de gulden snede (φ is ongeveer 1,61803... ), dan is de kleinere rechthoek gelijkvormig met zijn voorganger! Een rechthoek met deze lengte-breedteverhouding noemen we een gulden rechthoek. De kleinere gulden rechthoek kunnen we wéér verdelen in een vierkant en een nog kleinere gulden rechthoek.Op deze manier kun je telkens kleinere vierkanten afsplitsen, tot je uiteindelijk een microscoop nodig hebt om de kleinste vierkantjes nog te kunnen zien. Het zal je opgevallen zijn dat we in de figuur een spiraal door een aantal hoekpunten van de vierkanten hebben getekend. Deze soort spiralen komen in de natuur vaak voor als er sprake is van een gelijkvormige groei De spiraal in het plaatje hiernaast is een bijzonder geval: de spiraal van Fibonacci.
|
 De Gulden Snede blijkt vaak (soms in combinatie met de getallen van Fibonacci) in de natuur voor te komen. Zo kun je de Gulden Snede herkennen in de rangschikking van zonnepitten, de structuur van denneappels en de groei van bepaalde schelpen zoals de Nautilus schelp hiernaast. De doorsnede van de Nautilus is trouwens niet een spiraal van Fibonacci, maar een logaritmische spiraal. De Gulden Snede blijkt vaak (soms in combinatie met de getallen van Fibonacci) in de natuur voor te komen. Zo kun je de Gulden Snede herkennen in de rangschikking van zonnepitten, de structuur van denneappels en de groei van bepaalde schelpen zoals de Nautilus schelp hiernaast. De doorsnede van de Nautilus is trouwens niet een spiraal van Fibonacci, maar een logaritmische spiraal. |



