  The Golden Ratio, also known as the Golden Section, represents a ratio frequently encountered in nature. It divides a line or length into two unequal parts, such that the ratio of the smaller part to the larger part is the same as that of the larger part to the whole. The rectangle with sides a and b, remaining after removing the square with side a, is similar to the original rectangle. The ratio a/b is denoted by φ, called the golden number, and also referred to as the golden ratio. φ is approximately 1.61803398875. |
| The golden ratio is also called the "golden division" (sectio aurea), "golden rule" (ratio aurea), or "divine proportion" (proportio divina). The golden ratio is interesting for various reasons. Firstly, it is a classical belief that the golden ratio provides "beautiful" proportions. In ancient times, the Greeks based the designs of buildings on the golden ratio, whether consciously or not. Later, this concept became fashionable again in the Renaissance, and even today there are artists and architects who apply the golden ratio in their work to achieve a beautiful composition. |
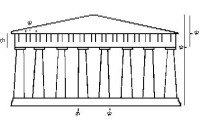  Examples from antiquity include:The famous Parthenon (temple of the Greek goddess Athena) was built around 440 BC. You can also find the Golden Ratio in it. |
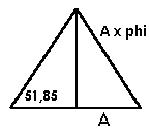
The ancient Egyptians built pyramids that were used as tombs. In addition to architectural research, mathematical investigations are also conducted. It turns out that the Golden Ratio plays a significant role in the construction of a pyramid. Let's take the Great Pyramid of Giza (built around 2500 BC) as an example. The slope angle of this pyramid is 51.85°. When we make a cross-section of the pyramid in the following way, we get a triangle. If you now give the base of the triangle a length of A, then the length of the slanted line is: A * phi. So, the Golden Ratio is also present in the pyramids.
|
| In classical painting, the golden ratio is also applied. It is used, for example, to determine the length-to-width ratio of a painting. The golden ratio is also used in defining the location of the focal point. |
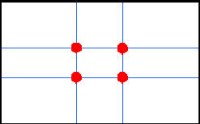  In the past, people had never heard of the golden ratio, yet they unconsciously composed their paintings on it. Naturally, the eye seeks out this point. In a rectangular plane, this point can be found in four places (see the red dots: top right, top left, bottom left, bottom right).Rectangles with this ratio and the corresponding squares are frequently found in the paintings of Piet Mondrian. Interestingly, Mondrian himself claimed never to have calculated his works. |
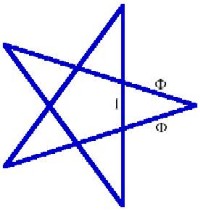 The Golden Ratio has several interesting mathematical properties:The Golden Ratio leads to a uniform plane division. The Golden Ratio appears in figures with pentagonal symmetry. Try drawing a regular pentagram. Each of the five triangles is an isosceles triangle where the sides are in the ratio of 1 : φ (= φ : 1). |
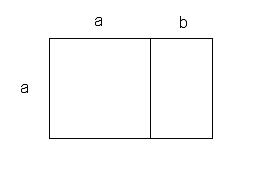
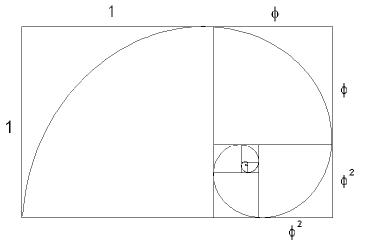 A particularly interesting rectangle is the golden rectangle. The golden ratio enables a unique plane division in this rectangle, where only squares of different sizes are used. Look at the image next to this text. We start with a rectangle with a length of 1 + φ and a width of 1. We cut away a square with a side length of 1 on the left side, leaving a rectangle with a length of 1 and a width of φ on the right. If φ is equal to the golden ratio (approximately 1.61803...), then the smaller rectangle is similar to its predecessor! A rectangle with this length-to-width ratio is called a golden rectangle. We can then divide the smaller golden rectangle again into a square and an even smaller golden rectangle.In this way, we can repeatedly divide smaller squares until we eventually need a microscope to see the smallest squares. You may have noticed that we drew a spiral passing through some of the vertices of the squares in the figure. These kinds of spirals are common in nature when there is uniform growth. The spiral in the image next to this text is a special case: the Fibonacci spiral.. |
 The Golden Ratio often appears in nature (sometimes in combination with Fibonacci numbers). You can recognize the Golden Ratio in the arrangement of sunflower seeds, the structure of pinecones, and the growth of certain shells like the Nautilus shell shown here. By the way, the cross-section of the Nautilus is not a Fibonacci spiral but a logarithmic spiral.. |